Benchmarking the Performance of Asset Management Banks

D.K. Malhotra
Thomas Jefferson University

Rashmi Malhotra
Saint Joseph’s University

Robert Nydick
Villanova University

This study utilized a data envelopment analysis model to study the performance persistence of 16 asset management institutions. When we evaluate performance based on capital efficiency (or productivity) ratio, earnings before interest, taxes, depreciation, and amortization (EBITDA) margin, and return on investment (ROI), we find that only one asset management bank has consistently outperformed its peers every year from 2014 to 2019. When we add tax efficiency, as measured by calculated tax rate, in addition to EBITDA, ROI, and capital efficiency ratio, we find that only 3 banks have consistently outperformed their peers inthe industry every year for the period ranging from 2014 to 2019. These consistent findings indicate that,
indeed, the skill of asset managers does play a role in asset management, at least in the short run.

Keyword: return on investment (ROI), earnings before interest, taxes, depreciation, and amortization (EBITDA),taxefficiency,andcapitalefficiency,performancepersistence,dataenvelopmentanalysis,asset management banks

INTRODUCTION

Asset management companies offer potential investors various types of investment products that match their risk-return profile at a reduced cost. Investors normally select an investment vehicle based on previous results, since they perceive the vehicle as a proof of the ability of the manager to achieve a higher rate of return. However, does past performance guarantee future performance? Past performance may be due to lack or increased risk-taking on the part of the asset manager and may not repeat in the future. Previous studies on mutual fund studies have analyzed the link between past and future performance and have found mixed evidence of continued performance. (Grinblatt & Titman 1992; Hendricks, Patel, and Zeckhauser 1993; Goetzmann and Ibbotson 1994; Elton, et al. (1996a); Gruber (1996); Carhart 1997; Wermers 2000; Davis 2001; Baras, et al. 2010; Budiono and Martens 2010). Further, previous research related to the performance of mutual funds did not find any evidence of mutual fund portfolio managers outperforming the return after adjusting for risk. (Friend, Blume, and Crockett, 1970; Lehmann and Modest 1987; Grinblatt and Titman, 1989, 1992).

This research examines asset management bank performance by benchmarking an asset management bank against each other to evaluate a bank’s relative efficiency. Data envelopment analysis (DEA) is used in three distinct methods in this study to investigate the performance persistence of asset management banks:

1. From 2014 to 2019, we compared each asset management bank’s performance with others to find asset management banks that consistently outperformed their counterparts year after year.
2. Secondly, we benchmark each asset management bank’s performance against its own performance in previous years to assess the trend in their performance relative to themselves.
3. Finally, we pooled the data of all asset management banks from 2014 to 2019 and benchmarked them against one another to determine the industry leaders across a six-year sample period.

The study is significant for several reasons. To begin with, the dollar quantity of assets managed by the asset management business has expanded multiple times, from $11.8 trillion at the end of 2010 to $26 trillion as of December 2019. (ICI)¹. Yet, to our knowledge, no empirical research exists that evaluates the performance persistence of asset management banks. Secondly, if some asset management banks do outperform others in the industry, this implies that the skill of manager does matter. Third, if asset manager skill is a factor in asset management bank success, outperforming asset management banks should see higher cash inflows. Finally, data envelopment analysis identifies asset management banks that are inefficient relative to their peers and indicates the areas that require improvement, thus, motivating them to improve their efficiency. This study is structured along the following lines: Section II examines prior studies that demonstrate how the data envelopment analysis model has been implemented in the banking industry; Section III describes the technique utilized; and Section IV analyzes the findings. Section IV outlines the data envelopment analysis methodology; Section V examines empirical findings of this study; and Section VI summarizes our findings.

PREVIOUS STUDIES

Data envelopment analysis (DEA) is commonly used to assess the effectiveness of comparable decision-making units. Previous research has shown that DEA may be used to analyze the performance of airlines, banks, hospitals, and other comparable decision-making units. Using DEA methodology, Dia, Golmohammadi, and Takouda (2020) analyzed the performance of six large Canadian banks. The study discovered that Canadian banks’ performance efficiency has decreased after the financial crisis of 2007. Since 2007, the revenue growth has taken the largest blow, as per the study. Sakouvogui’s (2020) research investigated the consistency of cost efficiency measures such as stochastic frontier analysis and data envelopment analysis while analyzing commercial banks in the US. The findings demonstrate that DEA and SFA efficiency metrics are sensitive to the banking industry’s heterogeneity concerns. To evaluate the banking operations based on different types of performance metrics a study by Chen, Chen, and Peng (2008) used a DEA framework. The study discovered that a DEA-based performance evaluation gives a comparable perspective of the firm’s well-being as a financial index’s analysis. The study was restricted to only one credit cooperative bank. Aghimien, Kamarudin, Hamid, and Noordin (2016) discovered that many Gulf Cooperation Council banks operated at a high degree of efficiency. Nonetheless, the data revealed inadequate resource management on the part of the managers. Yang (2009) evaluated the performance of a single Canadian bank’s 758 branches. The study discovered that branch networks in various geographic locations have varying efficiency ratings, with Quebec branches having the greatest efficiency score. In a study conducted by Halkos and Salamouis, the efficiency of Greek banks was assessed using the data envelopment analysis technique (2004). According to the findings of the study, relative to small banks, larger banks are more efficient. Using the DEA and Malmquist productivity indexes, Neal’s (2004) study found that regional banks in Australia were relatively inefficient, and diseconomies of scale arise quite fast when a bank’s size rises. Chen, Sun, and Peng (2005) created DEA and Malqueist productivity indices for Taiwanese banks before as well as after the formation of a holding company to benchmark commercial banks in Taiwan. Howland and Rowse (2006) studies relative efficiencies of a large Canadian and an American bank. Sufian (2007) differentiated technical, pure technical, and scale efficiencies while studying

the efficiency of Singapore banks. Lin, Shu, and Hsiao (2007) compared the relative managerial effectiveness of Taiwanese banks. The research utilized the Malmquist index to determine each bank’s competitiveness and management efficiency. Bergendahl and Lindblom (2008) investigated the relative effectiveness of Swedish savings banks in terms of service orientation. The study assessed the number of “service-efficient” savings banks in Sweden. The study also evaluated the savings banks’ average service efficiency.

Finally, we did not find any study that specifically dealt with the asset management banks. Thus, this research adds to the existing literature by benchmarking the relative performance of asset management banks, a very important component of the U.S. financial markets.

MODEL

TheDEA Model²

The DEA is a generalized approach to optimization that measures the relative effectiveness of different decision-making entities with a number of objectives (outputs) and a number of inputs. By assessing the effectiveness with which a decision-making unit (DMU) makes use of accessible assets (called inputs) to produce a given collection of outputs, the DEA assesses an entity’s performance.

The concept of effectivity or productiveness is defined in DEA methodology as a ratio of output generated relative to the inputs. To assess a DMU’s relative performance, DEA compares its efficiency to the efficiency of the most productive DMU or DMUs. The most efficient unit receives a one hundred percent effectiveness rating from the DEA model. Any DMU that has a score beneath 100% is inefficient relative to 100% efficient DMU. We consider n DMUs, m input variables, and r output variables to develop a DEA model as detailed below.

j = 1, 2, 3, …, n.

i = 1, 2, 3, …, m.

r = 1, 2, 3, …, s.

As a result, DMUs use the variables given below:

𝑋𝑖,𝑗 refers to the quantity of input i for the j^th decision-making unit.

𝑌𝑟,𝑗 refers to the quantity of output r for the j^th decision-making unit.

𝑢 𝑟 refers to weight r given to output.

𝑣𝑖 refers to weight given to input.

Charnes, Cooper, and Rhodes (1978) measured the efficiency of a DMU by allocating the most

desirable weights. Usually, the weights of all units are not equal. Instead, inputs and outputs may be assigned different weights. Equation 1 shows that the ratio of weighted output to weighted input determines how efficiently a decision-making unit processes inputs to generate outputs.

We can use a mathematical program to determine a weight set that maximizes a DMU’s efficiency if the efficiency of many DMUs (based on the same weight set) is restricted to a range of 0 and 1. The linear program choses weights so that only efficient decision-making units receive the upper bound rating of 1 or 100 percent efficiency. We use one of the DMUs as the assessment’s reference DMU to maximize efficiency. Further, we solve the model shown in equations 2 and 3 to determine the efficiency score for the other DMU.

E is an infinitesimal or non-Archimedean constant that keeps the weights from disappearing (Charnes et. al., 1994). Equation 2 illustrates the optimal objective function reflecting the utility of DMUo. Any entity with a score of 1 is 100 percent is relatively successful and will lie on the frontier of efficiency. Those decision-making units that score less than one are inefficient and, thus, fall below the performance frontier. To solve equation 2, each DMU serves as a reference decision making unit for determining the efficiency of the other decision-making units. Therefore, we can generate a Pareto efficiency estimate when all efficient entities are on the efficiency frontier(Thanassoulis, 2001). Byusing restrictions,=miioixv1=1,to normalize the denominator, we can easily convert the model in equations 2 and 3 into an equivalent linear program.Using the goal of maximizing the weighted sum of outputs given the restriction that the weighted sum of inputs is limited to one, we can devise the DEA model of output maximization as described in equations 4 and 5

The CCR (Charnes, Cooper, and Rhodes) model is used in this case. A generic input minimization CCR model, on the other hand, may be written as specified in equation 6.

Subject to

According to the fundamentals of linear programming, every linear program has a related linear program known as its dual. As a result, equation 8 depicts the dual maximization of DEA program output:

subject to

If * = 1, the present input levels cannot be lowered, suggesting that the o^th decision making unit is on the efficiency frontier. Otherwise, if * < 1, then the efficiency frontier dominates the o^th decision making unit. The efficiency level * indicates the o^th decision making unit’s input-oriented efficiency score. Further, an individual DMU’s input decrease is referred to as slack value. A model may have slack for input as well as output. (Equation 10)

We should solve the following linear program specified in equation 11 to discover any non-zero slacks after implementing the linear program (equation 10).

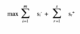
subject to

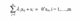
For all i and r, a decision-making unit is efficient if and only if * = 1 and si-*= sr+* = 0. A decision-making unit is inefficient if and only if * = 1 and si-*≠ 0 and (or) sr+* ≠ 0 for some i and r. Models (8) and (11), in fact, form a two-stage DEA process that describes the DEA model below:

DEA not only aims to differentiate productive entities from underperforming (sub-optimal) entities by using efficient entities as a “role model,” but the model also reveals the reasons why an entity may be performing at sub-optimal levels. Thus, the methodology allows investors to articulate their choices as to whether to invest with a specific asset management company. This also enables managers to identify vulnerable areas where relative productivity is utilized by DEA, a term that encourages firms to be compared with other recognized productive organizations. Furthermore, the DEA model establishes an efficiency frontier of efficient businesses that serves as a benchmark against the decision-making unit being compared. To attain efficiency, DMUs that are below the efficient frontier must enhance one of the input values without impacting the others.

DATA

To study the performance persistence in asset management companies, we used the financial performance indicators from financial statement data available from Mergent Online. Investors should be able to assess a company’s profitability in a variety of ways, such as how efficiently the organization uses resources and how much money the company generates from the managerial operations. Therefore, we used only those variables that evaluate financial performance of a company, namely earnings before interest, taxes, depreciation, and amortization (EBITDA) margin, return on investment (ROI), productivity of capital as measured by capital efficiency ratio, and effective annual tax rate. We explain the significance of each of these variables in evaluating the performance of asset management companies as follows. We used two models to benchmark the relative performance of 16 asset management banks³. In the first model, we used three variables—earnings before interest, taxes, depreciation, and amortization (EBITDA) margin, return on investment (ROI), and capital efficiency ratio (CER)⁴. In the second model, we introduce a fourth variable to assess the tax efficiency of asset managers by including calculated tax rate for an asset

management bank. We provide a list of the 16 asset management banks in appendix. Standard & Poor’s Industry Surveys for capital markets industry identifies these banks as competitors. Therefore, our study evaluates performance persistence based on:

• Earnings before interest, taxes, depreciation, and amortization (EBITDA)
• Return on investment (ROI)
• Capital efficiency ratio (CIR)
• Effective annual tax rate (EATR)

EBITDAis a measure of a company’s overall financial performance. EBITDA focuses on the operating performance of a company using core activities before considering the impacts of the capital structure, leverage, and non-cash products such as depreciation. Further, EBITDA is a metric that is a major indicator of a company’s performance and hence detrimental in assessing the efficiency score. In addition, EBITDA allows a potential investor to compare a company’s performance with its competitors or peers. Hence, by analyzing EBITDA across firms, a firm can readily compare the outcomes of its operational activities to those of its rivals and others in their industry. Therefore, the assessed margin gives analysts and investors a glimpse of short-term operational efficiency.

While EBITDA might provide a snapshot of a company’s growth, we do not get the complete picture. Thus, we should use EBITDA in conjunction with other business indicators such as return on investment.

ReturnonInvestment(ROI)is a metric used to assess the effectiveness of an investment or to compare the effectiveness of several investments. Having the vision to see if an investment will pay-off enables an investor to make financial decisions to develop his/her wealth effectively. ROI aims to calculate the amount of return on a single investment directly, compared to the cost of the investment. An indication of superior results is a higher ROI. Thus, we should use ROI as a maximizing production variable in our research.

Effectiveannual tax rate is the effective corporate tax rate that companies pay on their pre-tax profits. A higher tax rate indicates that the asset manager is not engaging in tax-efficiency practices. A lower tax indicates tax efficient asset management. Thus, we should use tax rate as a minimizing input. Investment taxes have a significant role for mutual fund investors, according to Jeffrey and Arnott (1993), Dickson and Shoven (1995), and Arnott, Kalesnik, and Schuesler (2018). Between 1990 and 2016, tax-efficient asset management methods used by U.S. equities mutual funds produced beneficial returns both after and before taxes (Sialm and Zhang, 2020). Malhotra, Martin, and Lafond (2011) looked at the features of tax-efficient mutual funds that an investor may utilize to make an informed decision

In addition, Sialm and Zhang (2020) studied the relationship between tax burden and mutual fund performance in recent research. They developed a model that introduces heterogeneous tax clienteles. They discovered that the performance of equities mutual funds in the United States is connected to their tax loads. In their analysis, tax efficient funds demonstrated not just greater after-tax performance, but also superior before-tax performance. Thus, tax rate can make a major contribution towards the efficiency factor of an asset management bank.

CapitalEfficiencyRatioof a company uses the contribution of a company’s capital to generate revenue for its shareholders as a measure of a company’s efficiency. Capital efficiency is the ratio of how much a company is using its resources on growing revenue and how much they are getting in return. At the most basic level, capital efficiency is an indicator of how well a firm uses its cash to function and develop more efficient measures. Further, investors should always check this ratio to ensure that the assets are being used effectively and that the company’s revenue is rising at a reasonable rate. This ratio is measured by dividing the total assets of a company by its sales. A higher ratio indicates that for every revenue dollar earned a company is using larger amount of total assets, while a lower ratio indicates that every revenue dollar uses fewer total assets. Thus, a lower ratio is an indicator of efficiency in generating revenue with fewer resources. Therefore, we should use capital efficiency ratio as an input variable that should be minimized.

Table 1 provides summary statistics of the data of the sixteen banks used for analysis.

TABLE1

SUMMARY STATISTICS OF THE FOUR VARIABLES USED AS INPUT AND OUTPUT IN THIS STUDY TO ANALYZE THE PERFORMANCE OF ASSET MANAGEMENT

BANKS FOR THE YEAR 2018

Companies\Variables	Return on Investment (%)	EBITDA Margin (%)	Effective Tax Rate	Capital Efficiency Ratio
2014
Mean	28.52	35.02	30.22	3.72
Standard Deviation	14.83	11.41	9.79	5.17
2015
Mean	26.36	33.51	33.62	3.89
Standard Deviation	16.66	10.28	11.77	5.19
2016
Mean	22.07	32.19	32.31	4.06
Standard Deviation	13.89	10.72	9.33	5.13
2017
Mean	23.79	34.43	24.71	3.95
Standard Deviation	14.21	12.29	23.80	4.44
2018
Mean	22.16	30.92	24.62	3.91
Standard Deviation	14.16	11.40	24.88	3.77
2019
Mean	20.22	30.12	22.77	3.86
Standard Deviation	17.32	14.98	15.99	3.17

As shown in Table 1, on average, asset management banks show

• A decline in ROI from 28.52% in 2014 to 20.22% in 2019,
• A decline in EBITDA from 35.02% in 2014 to 30.12% in 2019,
• A decline in calculated effective tax rate from 30.22% in 2014 to 22.77% in 2019; and
• An increase in capital efficiency ratio from 3.72 in 2014 to 3.86 in 2019, which points to reduced efficiency in using capital to generate revenue.

Data Envelopment Model Specifications for the Asset Management Industry

Various factors such as the choice of DMUs for a given DEA application, the choice of inputs and outputs, the choice of a DEA model for a certain application, and the choice of an appropriate sensitivity analysis technique widely impact the specifications of a DEA model (Ramanathan, 2003). The study’s findings, however, are dependent on the DEA model’s inputs and outputs. The selection of DMUs is influenced by two major factors: homogeneity and the quantity of DMUs. To effectively use the DEA approach, we should think about homogeneous units that do comparable activities and have similar goals. Meanwhile, the number of DMUs should be adequate to detect high-performing units and clearly define the input-output connection. Another important component of the efficiency analysis using DEA is the choice of input and output variables. The inputs should, in general, indicate the number of resources utilized or a component that should be minimized. Outputs indicate a variable that contributes to the company’s overall strength.

The model selection criteria in a DEA model are as follows:

a. The 16 asset management banks in this research are homogeneous since they are competitors according to S&P Industry Surveys on capital markets.

b. To correctly distinguish between productive and inefficient DMUs, the number of DMUs must be higher than the sum of the inputs and outputs. (Darrat et al., 2002; Avkiran, 2001). The total count of inputs and outputs should be at least twice the number of DMUs (Ramanathan, 2003).

c. Input and output selection criteria are frequently subjective. The starting point for DEA analysis is a comprehensive list of inputs and outputs that are judged essential to the study. Further, screening of inputs and outputs might be quantitative or judgmental (Saaty, 1980). DMUs often employ inputs as resources and they can also be interpreted as variables influencing DMU performance. Outputs, on the other hand, are the advantages generated by DMU operations and result in improved efficiency. If the number of inputs and outputs is drastically increased, a higher percent performance score (100 percent efficiency score) of a bigger number of DMUs would be attained, since DMUs become more specialized in order to be assessed in comparison to other DMUs (Ramanathan, 2003).

Finally, with options such as input maximization or output minimization, multiplier, or envelope, and constant or variable returns to scale, we can choose the required DEA model. The topic of DEA model orientation is discussed by Wade, Tone, and Zhu (2014). According to Wade, Tone, and Zhu (2014), a DEA study should spell out exactly what should be the major accomplishments. If the aim is to find out which units are wasting resources, then input reduction should be the main emphasis of the activity. In this case, the input-oriented DEA is more appropriate. Also, DEA applications with inflexible inputs or inputs that are not entirely controlled should utilize output-based formulations, whereas DEA applications with outputs that are the result of management objectives should use input-based formulations. In addition, using a certain version of DEA model is also an important parameter. We should utilize the multiplier version for an operation that stresses the importance of inputs and outputs. Likewise, envelopment models are more fitting for an application that considers connections between DMUs. Furthermore, the features of the application dictate whether constant or variable returns to scale are used. If the output of DMUs is significantly dependent on the scale of operations, constant returns to scale is preferable; otherwise, variable returns to scale is preferable.

The comparative assessment between asset management banks is a significant consideration in our research, and so we chose the envelopment models for in this study. Furthermore, the performance of DMUs is an outcome of management priorities, and thus we used an input-based formulation. In envelopment form, the DEA model structure frequently employs an equation and a separate computation for each input and output. In addition, both input and output variables can be utilized concurrently and computed in their own units.

EMPIRICALANALYSIS

Because each asset management bank is a homogeneous unit, we can use the DEA technique to generate an efficiency score for each DMU on a scale of 1 to 100 and compare their performance. We analyzed and computed the efficiency of these banks using the ratios for 2014-2019, and we evaluated the performance persistence with two different models. In the first model, we evaluated 16 asset management banks based on earnings before interest, taxes, depreciation, and amortization (EBITDA) margin, ROI, and capital efficiency ratio. In the second model, we also considered the tax efficiency of an asset management fund by including a fourth variable, effective annual tax rate, because ultimately investors will get after tax return on their investment.

TABLE 2

EFFICIENCY SCORES BASED ON DATA ENVELOPMENT ANALYSIS MODELS FOR THE

THE ASSET MANAGEMENT BANKS FOR EACH OF THE SIX YEARS FROM 2014 TO 2019

Banks\Year	2014	2015	2016	2017	2018	2019	Mean	Standard Deviation
Model 1: Efficiency based on EBITDA, ROI, and Capital Efficiency
AMG	32%	28%	24%	25%	33%	29%	28%	4%
AMP	7%	7%	7%	8%	10%	9%	8%	1%
BEN	48%	42%	38%	37%	44%	41%	42%	4%
BLK	5%	4%	5%	7%	9%	9%	7%	2%
BX	100%	15%	100%	100%	100%	100%	86%	35%
CNS	100%	97%	100%	100%	100%	100%	99%	1%
EV	60%	61%	64%	74%	63%	44%	61%	10%
FII	66%	69%	89%	90%	91%	80%	81%	11%
IVZ	23%	20%	17%	18%	19%	17%	19%	2%
LM	35%	34%	34%	36%	42%	37%	37%	3%
TROW	100%	100%	100%	100%	100%	100%	100%	0%
VRTS	59%	42%	35%	25%	22%	19%	34%	15%
SEIC	75%	73%	80%	85%	94%	82%	82%	8%
WDR	99%	85%	76%	81%	94%	84%	87%	9%
WETF	100%	100%	74%	92%	51%	30%	75%	29%
JHG	39%	43%	37%	35%	37%	31%	37%	4%
Model 2: Efficiency based on EBITDA, ROI, Effective Annual Tax Rate, and Capital Efficiency

AMG	53%	62%	71%	35%	69%	100%	65%	22%
AMP	50%	18%	100%	11%	47%	29%	42%	32%
BEN	57%	75%	87%	47%	54%	64%	64%	15%
BLK	74%	96%	87%	8%	56%	28%	58%	35%
BX	100%	100%	100%	100%	100%	100%	100%	0%
CNS	100%	100%	100%	100%	100%	100%	100%	0%
EV	65%	80%	86%	80%	78%	70%	77%	8%
FII	71%	87%	99%	100%	95%	87%	90%	11%
IVZ	42%	39%	64%	24%	41%	41%	42%	13%
LM	46%	59%	84%	46%	100%	37%	62%	25%
TROW	100%	100%	100%	100%	100%	100%	100%	0%
VRTS	66%	56%	75%	65%	35%	45%	57%	15%
SEIC	76%	81%	80%	87%	96%	82%	83%	7%
WDR	100%	96%	97%	87%	94%	84%	93%	6%
WETF	100%	100%	74%	94%	98%	81%	91%	11%
JHG	100%	100%	100%	43%	66%	60%	78%	25%

A company with 100% score is considered the most efficient and a company with less than 100% score is considered inefficient. In part A, efficiency scores are based on EBITDA margin, return on investment, and capital efficiency ratio. In part B, efficiency scores are based on EBITDA margin, return on investment, effective annual tax rate, and capital efficiency ratio.

Table 2 shows that, based on the first model, T. Rowe Price Group Inc. (NYS: TROW) was the only asset management bank that was 100% efficient through the entire sample period relative to its peers, and Blackstone Group (NYS: BX) and Cohen & Steers (NYS: CNS) were 100% efficient relative to their peers for every year from 2014-2019 except 2015. The least efficient asset management bank relative to its peers was BlackRock Inc. (NYS: BLK) with efficiency scores ranging from 5-9% (average = 7%) and a standard deviation of 2%; BLK was very closely followed by Affiliated Managers Group Inc. (AMG), with an average efficiency score of 7% and standard deviation of 1%. Model 1 also shows that four asset management banks—BX, CNS, TROW, and WisdomTree Investments Inc. (NMS: WETF)—were 100% efficient in 2014, but only two, TROW and WETF, were 100% efficient relative to their peers in 2015. Since 2016, three banks (BX, CNS, and TROW) have been consistently 100% efficient relative to their peers based on EBITDA margin, ROI, and capital efficiency ratio.

Table 2 also shows that, based on the second model, three asset management banks (BX, CNS, and TROW) scored 100% efficiency relative to their peers for each year of the study period. On an average, the least efficient asset management banks were AMP and IVZ with an average efficiency score of 42% for the sample period of 2014-2019. Four asset management banks were 100% efficient relative to their peers in 2019. AMG, BX, CNS, and TROW were 100% efficient relative to other asset management banks for the year 2019. Out of 16 asset management banks in the sample, 13 banks (AMP, BEN, BLK, BX, EV, FII, IVZ, LM, VRTS, SEIC, WDR, WETF, and JHG) were inefficient relative to their peers when evaluated

based the second model, performing significantly less than 100% efficient relative to their peers. The least efficient asset management bank was BLK with an efficiency score of only 27% relative to its peers, followed by AMP with a score of 29%, and LM with a score of 37%. Model 2 also shows that 6 asset management banks (BX, CNS, TROW, WDR, WETF, and JHG) had a 100% efficiency score relative to their peers in 2014.

For three assets management banks (BX, CNS, TROW), past performance has been a predictor of continued good performance. Meanwhile, IVZ has been the least efficient bank relative to its peers for each year of the sample, and therefore, past performance is also a predictor of future poor performance for IVZ based on EBITDA, ROI, effective annual tax rate, and capital efficiency ratio.

Table 3 ranks asset management companies based on their average efficiency scores for the years 2014- 2019. Part A in Table 3 rank is based on EBITDA, ROI, and capital efficiency ratio and part B rank is based on EBITDA, ROI, effective annual tax rate, and capital efficiency ratio.

TABLE3

RANKING OF 16 ASSET MANAGEMENT BANKS BASED ON EFFICIENCY SCORES ON YEARLY BASIS FROM 2014 TO 2019

	2014		20.15		2016		2017		2018		2019
CNS	100%	TROW	100%	JHG	100%	FII	100%	TROW	100%	BX	100%
JHG	100%	CNS	100%	AMP	100%	CNS	100%	CNS	100%	CNS	100%
TROW	100%	JHG	100%	BX	100%	TROW	100%	BX	100%	TROW	100%
WETF	100%	WETF	100%	AMG	100%	BX	100%	LM	100%	FII	87%
BX	100%	BX	100%	TROW	100%	WETF	94%	WETF	98%	WDR	84%
WDR	100%	BLK	96%	CNS	100%	SEIC	87%	SEIC	96%	SEIC	82%
SEIC	76%	WDR	96%	FII	99%	WDR	87%	FII	95%	WETF	81%
BLK	74%	FII	87%	WDR	97%	EV	80%	WDR	94%	EV	70%
FII	71%	SEIC	81%	BLK	87%	AMG	71%	EV	78%	AMG	69%
VRTS	66%	EV	80%	BEN	87%	VRTS	65%	JHG	66%	BEN	64%
EV	65%	BEN	75%	EV	86%	BEN	47%	BLK	56%	JHG	60%
BEN	57%	AMG	62%	LM	84%	LM	46%	BEN	54%	VRTS	45%
AMG	53%	LM	59%	SEIC	80%	JHG	43%	AMP	47%	IVZ	41%
AMP	50%	VRTS	56%	VRTS	75%	IVZ	24%	IVZ	41%	LM	37%
LM	46%	IVZ	39%	WETF	74%	AMP	11%	VRTS	35%	AMP	29%
IVZ	42%	AMP	18%	IVZ	64%	BLK	8%	AMG	35%	BLK	28%
Part B: Efficiency scores based on EBITDA, ROI, effective annual tax rate, and capital efficiency ratios
CNS	100%	TROW	100%	CNS	100%	CNS	100%	TROW	100%	BX	100%
TROW	100%	WETF	100%	TROW	100%	TROW	100%	CNS	100%	CNS	100%
WETF	100%	CNS	97%	BX	100%	BX	100%	BX	100%	TROW	100%
BX	100%	WDR	85%	FII	89%	WETF	92%	WDR	94%	WDR	84%
WDR	99%	SEIC	73%	SEIC	80%	FII	90%	SEIC	94%	SEIC	82%
SEIC	75%	FII	69%	WDR	76%	SEIC	85%	FII	91%	FII	80%
FII	66%	EV	61%	WETF	74%	WDR	81%	EV	63%	EV	44%
EV	60%	JHG	43%	EV	64%	EV	74%	WETF	51%	BEN	41%
VRTS	59%	VRTS	42%	BEN	38%	BEN	37%	BEN	44%	LM	37%
BEN	48%	BEN	42%	JHG	37%	LM	36%	LM	42%	JHG	31%

JHG	39%	LM	34%	VRTS	35%	JHG	35%	JHG	37%	WETF	30%
LM	35%	AMG	28%	LM	34%	AMG	25%	AMG	33%	AMG	29%
AMG	32%	IVZ	20%	AMG	24%	VRTS	25%	VRTS	22%	VRTS	19%
IVZ	23%	BX	15%	IVZ	17%	IVZ	18%	IVZ	19%	IVZ	17%
AMP	7%	AMP	7%	AMP	7%	AMP	8%	AMP	10%	BLK	9%
BLK	5%	BLK	4%	BLK	5%	BLK	7%	BLK	9%	AMP	9%

Part A ranks are based on EBITDA, ROI, and capital efficiency ratio. Part B ranks are based on EBITDA, ROI, effective annual tax rate, and capital efficiency ratio.

Part A and part B of Table 3 show that ranks for asset management companies differed on a yearly basis except for TROW, which consistently performed better relative to peers throughout the sample period. All other asset management banks continued to change ranks on a year-to-year basis. The wide difference in the efficiency scores of different asset management companies showed that skill of management in managing money matters, because some are significantly more efficient relative to others.

We also ranked each of the sixteen asset management banks based on performance index. Performance index for each asset management bank was constructed by dividing the standard deviation of efficiency scores by the average efficiency score for each bank over the sample period of 2014-2019. The bank with the lowest performance index score was the most efficient bank, because they have the lowest coefficient of variation in efficiency scores per unit of the efficiency score. Table 4 summarizes rankings for asset management banks based on performance index of a bank from 2014 to 2019. Based on mean efficiency score and standard deviation, we also computed the performance index as standard deviation divided by mean efficiency score for each asset management bank.

TABLE4

PERFORMANCE INDEX OF THE 16 ASSET MANAGEMENT BANKS FOR 2018.

Bank\Variables	Mean Efficiency Score	Standard Deviation	Performance Index	Bank\Symbol	Mean Efficiency Score	Standard Deviation	Performance Index
CNS	100%	0%	0.00	TROW	100%	0%	0.00
BX	100%	0%	0.00	CNS	99%	1%	0.01
TROW	100%	0%	0.00	LM	37%	3%	0.08
WDR	93%	6%	0.07	SEIC	82%	8%	0.09
SEIC	83%	7%	0.08	BEN	42%	4%	0.10
EV	77%	8%	0.10	WDR	87%	9%	0.10
WETF	91%	11%	0.12	JHG	37%	4%	0.11
FII	90%	11%	0.12	IVZ	19%	2%	0.11
IVZ	42%	13%	0.30	AMG	28%	4%	0.13
BEN	64%	15%	0.23	FII	81%	11%	0.14
VRTS	57%	15%	0.26	AMP	8%	1%	0.16
AMG	65%	22%	0.33	EV	61%	10%	0.16

LM	62%	25%	0.40	BLK	7%	2%	0.30
JHG	78%	25%	0.32	WETF	75%	29%	0.39
BLK	58%	35%	0.59	BX	86%	35%	0.41
AMP	42%	32%	0.76	VRTS	34%	15%	0.45

Table 3: Ranking of individual company is based on the DEA efficiency scores from Table 3. Highest ranking is given to a company with the efficiency score of 100. Model 1 is based on EBITDA, ROI, and capital efficiency ratio. Model 2 is based on EBITDA, ROI, effective annual tax rate, and capital efficiency ratio.

Table 4 shows that CNS, BX, and TROW had the lowest performance index and they were the most efficient asset management banks, followed closely by WDR, SEIC, and EV with efficiency scores of 0.07, 0.08, and 0.10, based on EBITDA, ROI, and capital efficiency ratio. On average, AMP was the least efficient bank with a performance index of 0.76, followed by BLK with a performance index of 0.59.

Figures 1a and 1b show the efficiency frontier of asset management banks for the year 2019. Figure 1a shows efficiency frontier for 16 asset management banks based on model 1. Figure 1b shows the efficiency frontier for 16 asset management banks based on model 2. Blue dots on the efficiency frontier represent 100% efficient companies, whereas the red dots that lie below the efficiency frontier are inefficient companies. By calculating the difference between the efficiency frontier and the inefficient asset management banks, the DEA Analyzer measured the degree of inefficiency. This efficiency frontier may be used by an investor to evaluate the relative efficiency of an asset management bank throughout the industry.

FIGURE 1A

EFFICIENCY FRONTIER FOR ASSET MANAGEMENT BANKS BASED ON BITDA ,ROI, CAPITAL INTENSITY RATIO, AND TAX RATE FOR 2019 (MODEL 1)

FIGURE 1B

EFFICIENCY FRONTIER FOR ASSET MANAGEMENT BANKS BASED ON BITDA,ROI, CAPITAL ITENSITY RATIO, AND TAX RATE FOR 2019

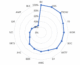
The efficiency scores are shown in percentage value varying from 0-100%. We found that, based on model 1, the efficiency of BX, CNS, and TROW was 100% and they were on the efficiency frontier; all other companies were below the efficiency frontier. Figure 1b shows that, based model 2, BX, CNS, and TROW were on the efficiency frontier with 100% efficiency.

We then computed the peers for inefficient companies so that inefficient companies could learn from their efficient peers and improve their performance. Peers for inefficient companies were computed based on model 1 and model 2 for the year 2019 (Table 5).

TABLE5

PEER COMPANIES AND THEIR WEIGHTS IN PERCENTAGE

Symbol	efficiency	AMG	BX	CNS
Peers based on EBITDA, ROI, Tax Rate, and Capital Efficiency Ratio
AMP	29%	0.83	0.03	0.15	1.00
BEN	64%	0.23	0.00	0.77	1.00
BLK	28%	0.63	0.13	0.23	1.00
EV	70%	0.24	0.00	0.76	1.00
FII	87%	0.04	0.00	0.96	1.00
IVZ	41%	0.55	0.00	0.45	1.00
LM	37%	0.00	0.00	1.00	1.00
VRTS	45%	0.52	0.00	0.48	1.00

SEIC	82%	0.00	0.00	1.00	1.00
WDR	84%	0.00	0.00	1.00	1.00
WETF	81%	0.70	0.00	0.30	1.00
JHG	60%	0.38	0.00	0.62	1.00
Peers based on EBITDA, ROI, and Capital Efficiency Ratio
Symbol	efficiency	CNS
AMG	29%	1.00			1.00
AMP	9%	1.00			1.00
BEN	41%	1.00			1.00
BLK	9%	1.00			1.00
EV	44%	1.00			1.00
FII	80%	1.00			1.00
IVZ	17%	1.00			1.00
LM	37%	1.00			1.00
VRTS	19%	1.00			1.00
SEIC	82%	1.00			1.00
WDR	84%	1.00			1.00
WETF	30%	1.00			1.00
JHG	31%	1.00			1.00

This table shows those companies that can serve as a benchmark for companies with DEA efficiency score of less than 100.

Table 5 shows that, based on EBITDA, ROI, and capital efficiency ratio, CNS serves as peer for 13 inefficient asset management banks for the year 2019. The inefficient banks should emulate CNS to improve their performance so that they can be on the 100% efficiency frontier.

When we determined the peers for inefficient companies based on model 2, we found that AMG, BX, and CNS were the peers for 12 inefficient companies for 2019: CNS was the peer for 12 companies, AMG was the peer for 9 companies, and BX was the peer for 2 companies. CNS was the 100% peer for LM, SEIC, and WDR, which means that LM, SEIC, and WDR needed to emulate 100% CNS. For FII, CNS served as a major peer with a score of 96%, and AMG was a small peer with a score of 4%. BX served as a small peer for AMP (3%) and BLK (13%). AMG was the peer for all inefficient banks except LM, SEIC, and WDR. The efficient peer companies had a comparable mix of input-output levels, but at a higher absolute level, than the inefficient company. In general, efficient businesses produced more than the company in question. Because of the characteristics of efficient peer firms, they were quite beneficial. as role models for inefficient businesses to learn from in order to enhance their performance.

Once, we know the inefficient banks, we should find out the areas where they lagged their efficient peers so that the inefficient banks could focus on improving their performance on those areas of shortfalls.

As a result, we calculated the slack variables to pinpoint the areas where inefficient firms trailed efficient firms. Table 6 summarizes the results of slack variables for the inefficient companies based on model 2 as well as based on model 1 for the year 2019.

TABLE6

SLACK VARIABLES OR INEFFICIENT ASSET MANAGEMENT BANKS \ FOR THE YEAR 2019

Sym bol	effici ency	Calculated Tax Rate %	Capital Efficiency	EBITDA Margin %	ROI %	efficiency	Capital Efficiency	EBITDA Margin %	ROI%
	Slack variables based on tax rate, capital efficiency ratio, EBITDA, and ROI	Slack variables based on capital efficiency ratio, EBITDA margin, ROI
AMG	100%	0.00	0.00	0.00	0.00	29%	2.55	33.76	68.94
AMP	29%	0.00	9.21	42.40	52.93	9%	10.09	43.25	70.91
BEN	64%	5.04	1.48	25.73	63.61	41%	1.48	32.82	67.06
BLK	28%	0.16	10.09	33.20	69.00	9%	10.09	41.13	71.70
BX	100%	0.00	0.00	0.00	0.00	100%	0.00	0.00	0.00
CNS	100%	0.00	0.00	0.00	0.00	100%	0.00	0.00	0.00
EV	70%	2.56	1.31	22.81	60.92	44%	1.31	31.14	65.45
FII	87%	2.50	0.26	19.72	44.65	80%	0.26	21.89	47.08
IVZ	41%	4.02	4.86	37.31	71.30	17%	4.86	41.83	72.31
LM	37%	50.53	1.76	42.48	72.41	37%	1.76	42.48	72.41
TROW	100%	0.00	0.00	0.00	0.00	100%	0.00	0.00	0.00
VRTS	45%	3.37	4.24	34.11	70.96	19%	4.24	40.34	72.14
SEIC	82%	5.48	0.23	20.70	50.48	82%	0.23	20.70	50.48
WDR	84%	4.52	0.20	30.67	60.09	84%	0.20	30.67	60.09
WETF	81%	0.00	0.65	46.71	39.67	30%	2.43	43.42	70.66
JHG	60%	1.99	2.31	28.15	66.81	31%	2.31	36.40	69.84

As shown in Table 6, AMP lagged in capital efficiency ratio, EBITDA margin, and ROI in both models. BEN, BLK, EV, FII, IVZ, LM, VRTS, SEIC, WDR, and JHG needed to improve in all four areas, tax rate, capital efficiency ratio, EBITDA margin, and ROI. Out of all the inefficient banks, LM needed maximum improvement in tax efficiency. LM also needed maximum improvement in ROI, followed closely by IVZ and VRTS.

Finally, we compare each asset management bank’s performance to its own performance in prior years to analyze the trend in their performance compared to themselves and to estimate their average efficiency from 2014 to 2019. Table 7 highlights the benchmarking of asset management banks against themselves from 2014 to 2019.

TABLE7

BENCH MARKING ASSET MANAGEMENT BANKS AGAINST THEMSELVES OVERTHE YEARS 2014 TO 2019

	2014	2015	2016	2017	2018	2019	Average
Model 1
AMG	100.00%	100.00%	81.11%	100.00%	79.80%	100.00%	93.49%
AMP	100.00%	93.55%	94.22%	88.89%	100.00%	100.00%	96.11%
BEN	100.00%	99.63%	96.84%	71.70%	75.47%	100.00%	90.61%
BLK	100.00%	100.00%	85.55%	100.00%	89.12%	100.00%	95.78%
BX	100.00%	70.83%	87.50%	100.00%	29.17%	100.00%	81.25%
CNS	100.00%	100.00%	100.00%	96.50%	82.80%	100.00%	96.55%
EV	100.00%	100.00%	100.00%	100.00%	79.08%	100.00%	96.51%
FII	84.21%	96.16%	100.00%	100.00%	84.54%	100.00%	94.15%
IVZ	100.00%	100.00%	100.00%	100.00%	65.38%	100.00%	94.23%
LM	100.00%	100.00%	100.00%	99.97%	100.00%	90.00%	98.33%
TROW	100.00%	100.00%	96.79%	100.00%	100.00%	100.00%	99.47%
VRTS	100.00%	73.13%	93.53%	100.00%	29.85%	100.00%	82.75%
SEIC	100.00%	98.42%	100.00%	100.00%	100.00%	100.00%	99.74%
WDR	100.00%	91.46%	90.69%	100.00%	75.89%	100.00%	93.01%
WETF	100.00%	100.00%	71.44%	81.03%	42.70%	100.00%	82.53%
JHG	100.00%	100.00%	80.00%	100.00%	100.00%	60.00%	90.00%
Model 2
AMG	100.00%	99.59%	79.72%	100.00%	79.80%	84.38%	90.58%
AMP	100.00%	93.55%	94.22%	88.89%	100.00%	100.00%	96.11%
BEN	100.00%	92.45%	77.36%	71.70%	75.47%	75.47%	82.08%
BLK	67.69%	68.35%	63.21%	100.00%	89.12%	100.00%	81.40%
BX	100.00%	70.83%	87.50%	100.00%	29.17%	100.00%	81.25%
CNS	100.00%	100.00%	100.00%	96.50%	82.80%	100.00%	96.55%
EV	100.00%	94.67%	94.23%	100.00%	76.32%	57.52%	87.12%

When compared to prior years, SEIC (99.74%) leads in terms of consistency of performance, followed by TROW (99.47%) from 2014 to 2019. Model 1 also reveals that BX has the lowest performance consistency (81.25%), followed by WETF, which has an average performance efficiency of 82.53 percent. Consistent with previous research on mutual funds (Sialm and Zhang, 2020), we discovered that SEIC and TROW had the highest consistency of performance on an after-tax basis, with an average efficiency score of 99.67 percent and 99.15 percent, respectively. Model 2 also reveals that, on an after-tax basis,

VRTS has the lowest consistency of performance with an average efficiency score of 64.68 percent, closely followed by WETF with an average efficiency score of 69.25 percent.

Finally, we combined all the data in one large pool to benchmark each bank against the rest of the banks using each observation as a single decision-making unit. Table 8 displays the winners and losers in the combined pool using model 1 and model 2. Using Model 1, BX (2017, 2019), WETF (2014, 2015), TROW

(2014, 2017, 2019), JHG (2014, 2015), CNS (2014), and WDR (2014) lead the pack with 100%

efficiency.While BLK (2014, 2015, 2016, 2017, 2018) has relative efficiency performance in single digits.

Likewise, using Model 2, BX (2017), WETF (2014, 2015), CNS (2019), TROW (2014, 2017, 2019) are

100% efficient, while AMP (2014, 2015, 2016, 2017, 2018, 2019) and BLK (2014, 2015, 2017, 2018, 2019)

trail behind with single digit efficiency values. In addition, we also calculated the peer weight factor for peer banks in the pool by adding peer weights for each bank not on the efficiency frontier. Model 1 was used to determine the net peer weight for banks with best practices, as shown in Table 9. WETF (2014) is the leader with the highest weight factor (35.70), followed by WETF (2015) – 28.49, and TROW (2017) –

24.80. In a similar manner, Table 10 illustrates the net peer weight for banks that adhere to best practices, employing Model 2. The major peer in this case is WETF (2015), carrying a weight factor of 85.71. Thus, consistent with our previous findings WETF is the most efficient bank in years 2014 and 2015.

TABLE8

BENCH MARKING ASSET MANAGEMENT BANKS AGAINST THEMSELVES OVERTHE YEARS 2014 TO 2019 IN A COMBINED POOL

Model1	Model 2
Symbol	efficiency	Symbol	efficiency
BX2017	100%	BX2017	100%
WETF2014	100%	WETF2014	100%
BX2019	100%	CNS2019	100%
TROW2019	100%	TROW2019	100%
CNS2019	100%	TROW2017	100%
JHG2014	100%	WETF2015	100%
TROW2017	100%	TROW2014	100%
WETF2015	100%	AMP2018	8%
JHG2015	100%	AMP2019	8%
TROW2014	100%	BLK2019	8%
CNS2014	100%	AMP2017	7%
WDR2014	100%	AMP2014	7%
BLK2018	9%	AMP2015	7%
BLK2017	8%	AMP2016	7%

BLK2014	7%	BLK2018	6%
BLK2015	7%	BLK2017	5%
BLK2016	7%	BLK2014	4%
		BLK2015	4%
		BLK2016	4%

TABLE9

BENCHMARKINGASSETMANAGEMENTBANKSAGAINSTTHEMSELVESOVERTHE YEARS 2014 TO 2019 IN A COMBINED POOL – PEER WEIGHT FACTOR (MODEL 1)

Symbol	PWF
WETF2014	35.70213
WETF2015	28.48611
BX2017	1.076386
TROW2017	24.79927
BX2019	1.083721
CNS2019	1.011388
TROW2019	1.840991

TABLE10

BENCHMARKING ASSET MANAGEMENT BANKS AGAINST THEMSELVES OVERTHE YEARS 2014 TO 2019 IN A COMBINED POOL – PEER WEIGHT FACTOR (MODEL 2)

Symbol	PWF
WETF2015	85.70563
BX2017	1.171158
TROW2017	4.365605
CNS2019	1.011388
TROW2019	2.746219

SUMMARY AND CONCLUSIONS

As the baby boomer generation prepares for retirement through savings, demand for investment vehicles rises. As a result, investors look for those investment alternatives that can help them grow their money over a period consistent with their investment objectives. Investment companies manage more than

$26 trillion in assets on behalf of 100 million retail investors in the United States. Investment companies manage about 23% of U.S. households financial assets (https://www.icifactbook.org/ch2/20_fb_ch2#reliance). Typically, and not surprisingly, past performance is used as a guiding criterion by investors to select investment. Investors also regard previous success as confirmation of management competence and put their capital to work accordingly. However, prior risk- taking may not continue to pay off in the future. Past performance can also be influenced by luck, whether good or poor. Many studies of investment firms have examined the link between past and future performance and have typically discovered some indication of performance persistence across short time horizons. In this study, we evaluated the performance of asset management banks over a six-year period. Note that the study is the first to benchmark the relative performance of asset management banks.

Using DEA, a non-parametric, performance measurement technique that enables managers to perform efficiency analysis of investment management services, this study evaluated the relative efficiency of 16

asset management banks for 2014 to 2019. There are several implications of our findings. First, individual investors typically select investment vehicles based on previous performance, as prior success is seen as proof of a manager’s competence to manage assets. But is previous performance a guarantee of future performance? The topic of previous success in mutual funds as a forecast of future performance has piqued the interest of practitioners, academics, and investors. Several studies have been conducted to investigate the link between past and future performance in the context of mutual funds, with various degrees of success. In this study, we discovered that some asset management institutions outperformed others in the industry year after year during a six-year period. Thus, the study’s findings can be regarded as proof that the asset manager’s skill may play a role in determining this consistent performance, at least in the short run.

Secondly, for investors, investment taxes play a vital role. The study also discovered that asset management banks that performed well pre-tax also performed well post-tax. Again, this is consistent with recent findings of Sialm and Zhang (2020). We discovered that asset managers that are efficient in generating returns with their investors’ cash are also efficient in saving them taxes through improved tax efficiency.

Finally, on a pre-tax basis, certain banks were not 100 percent efficient, but they were 100 percent efficient after taxes. Because taxes have an influence on an investor’s return, investors should analyze an asset manager’s performance after taxes and invest with asset management firms that are efficient after taxes.

DEA uses relative performance, a term that enables companies with a pool of proven productive companies to be used as a benchmark. The DEA model relates a firm to the pool of productive firms and a tolerance cap by building a productivity frontier of successful firms. The DEA model also demonstrates that firms that are below the productivity boundary and somewhat inefficient can be on the efficiency frontier by increasing one of the input values without harming the others. We found that, of the 16 asset management banks, only 4 were 100% efficient and 3 scored 95% or more on the efficiency scorecard on the basis of return on assets, EBITDA margin, revenue per employee, effective tax rate, interest coverage ratio, and capital efficiency. We also demonstrated the areas in which inefficient firms fall behind efficient firms.

Performance persistence due to money manager’s skill is a topic that has consistently attracted the attention of academic world. This study focused on the relative performance of asset management companies. Future studies should explore the relative performance and performance persistence of mutual funds. If some funds consistently outperform other funds over a certain time, it will be evidence that fund manager’s stock selection skill is important in generating a superior rate of rate of return.

ENDNOTES

^1.  https://www.ici.org/pdf/2020_factbook.pdf

^2. Ramanathan (2003) and Zhu (2003) are the primary sources for the DEA Model description used in this study.

^3.  Sixteen asset management banks in our sample are Affiliated Managers Group (AMG), Ameriprise Financial, Inc. (AMP), Franklin Resources, Inc. (BEN), BlackRock, Inc. (BLK), Blackstone Group, LP (BX), Calamos Asset Management Inc (CLMS), Cohen & Steers Inc (CNS), Eaton Vance Corp (EV), Federated Investors Inc (PA) (FII), Invesco Ltd (IVZ), Legg Mason, Inc. (LM), T.Rowe Price, Inc. (TROW), Virtus Investment Ptnrs Inc. (VRTS), SEI Investments Company (SEIC), Waddell&Reed Financial, Inc.(WDR), WisdomTree Investments, Inc. (WETF), Janus Capital Group, Inc. (JHG)

^4.  Academics have debated the use of ratio data in DEA models for a long time. Ratio measurements are utilized to directly represent inputs or outputs rather than as a complement to volume measures in some applications. In the banking industry, for example, performance analysis typically focuses on metrics such as the equity capital to asset ratio, net charge-offs to loans, and return on assets. (Olesen, Peterson, and Podinovsky, 2015). Furthermore, managerial choices are always made using ratio analysis. As a result, in this article, we employ ratios to assess the performance of asset management banks.

REFERENCES

Aghimien, P.A., Kamarudin, F., Hamid, M., & Noordin, B. (2016). Efficiency of gulf cooperation council banks: Empirical evidence using data envelopment analysis. ReviewofInternationalBusinessand Strategy, 26(1), 118–136. Retrieved from https://login.proxy1.lib.tju.edu/login?url=https://www- proquest-com.ezproxy.philau.edu/scholarly-journals/efficiency-gulf-cooperation-council- banks/docview/1990834904/se-2?accountid=28402

Arnott, R.D., Kalesnik, V., & Schuesler, T. (2018). Is your alpha big enough to cover its taxes? A quarter- century retrospective. Journal of Portfolio Management, 44, 78–102.

Bergendahl, G., & Lindblom, T. (2008). Evaluating the performance of Swedish savings banks according to service efficiency. European Journal of Operational Research, 185(3), 1663–1673.

Charnes, A., Cooper, W., & Rhodes, E. (1978). Measuring efficiency of decision-making units. European Journal of Operational Research, 2, 429–444.

Chen, T., Chen, C., & Sin-Ying, P. (2008). Firm operation performance analysis using data envelopment analysis and balanced scorecard: A case study of a credit cooperative bank. InternationalJournal of Productivity and Performance Management, 57(7), 523–539. http://dx.doi.org.ezproxy.philau.edu/10.1108/17410400810904010.

Chen, Y., Sun, L., & Peng, C. (2005). Commercial banks’ performance in Taiwan. InternationalJournal of Performance Management, 7(4), 444–463.

Cook, W.D., Tone, K., & Zhu, J. (2014). Data envelopment analysis: Prior to choosing a model. Omega, 44, 1. Retrieved from https://login.proxy1.lib.tju.edu/login?url=https://www-proquest- com.ezproxy.philau.edu/scholarly-journals/data-envelopment-analysis-prior-choosing- model/docview/1476855903/se-2?accountid=28402

Dia, M., Golmohammadi, A., & Takouda, P.M. (2020). Relative efficiency of canadian banks: A three- stage network bootstrap DEA. Journal of Risk and Financial Management, 13(4), 68. http://dx.doi.org.ezproxy.philau.edu/10.3390/jrfm13040068

Dickson, J.M., & Shoven, J.B. (1995). Taxation and mutual funds: An investor perspective. TaxPolicy and the Economy, 9, 151–180.

Farrell, M. (1957). The measurement of productive efficiency. JournaloftheRoyalStatisticalSociety, series A, 253–281.

Halkous, G., & Salamouris, D. (2004). Efficiency measurement of the Greek commercial banks with the use of financial ratios: A data envelope analysis approach. Management Accounting Research, 15(2), 201–224.

Howland, M., & Rowse, J. (2006). Measuring bank branch efficiency using data envelopment analysis: Managerial and implementation issues. INFOR, 44(1), 49–63.

Jeffrey, R.H., & Arnott, R.D. (1993). Is your alpha big enough to cover its taxes? JournalofPortfolio Management, 19, 15–25.

Lin, H., George, J., & Hsiao, C. (2007). Measuring efficiency of domestic banks in Taiwan: Application of data envelopment analysis and Malmquist index. AppliedEconomicsLetters, 14(11), 821–827.

Malhotra, D.K., Martin, R., & Lafond, A. (2011). Mutual fund tax efficiency and investment selection.

JournalofPersonalFinance, 10(2), 66–94.

Neal, P. (2004). X-Efficiency and Productivity Change in Australian Banking. AustralianEconomic Papers, 43(2), 174–191.

Olesen, O.B., Petersen, N.C., & Podinovski, V.V. (2015). Efficiency analysis with ratio measures.

EuropeanJournalofOperationalResearch, 245(2), 446–462. Retrieved from https://login.proxy1.lib.tju.edu/login?url=https://www-proquest- com.ezproxy.philau.edu/scholarly-journals/efficiency-analysis-with-ratio- measures/docview/1682700753/se-2?accountid=28402

Sakouvogui, K. (2020). A comparative approach of stochastic frontier analysis and data envelopment analysis estimators: Evidence from banking system. JournalofEconomicStudies, 47(7), 1787– 1810. http://dx.doi.org.ezproxy.philau.edu/10.1108/JES-01-2019-0051

Sialm, C., & Zhang, H. (2020). Tax‐Efficient asset management: Evidence from equity mutual funds. The Journal of Finance, 75(2), 735–777. http://dx.doi.org.ezproxy.philau.edu/10.1111/jofi.12843

Sufian, F. (2007). Trends in the efficiency of Singapore’s commercial banking Groups A non-stochastic frontier DEA window analysis approach. InternationalJournalofProductivityandPerformance Management, 56(2), 99–135.

Troutt, M., Rai, A., & Zhang, A. (1996). The potential use of DEA for credit applicant acceptance systems. Computers and Operations Research, 4, 405–409.

Yang, Z. (2009). Assessing the performance of canadian bank branches using data envelopment analysis. The Journal of the Operational Research Society, 60(6), 771–780. http://dx.doi.org.ezproxy.philau.edu/10.1057/palgrave.jors.2602619.

Zhu, J. (2003). Quantitative Models for Performance Evaluation and Benchmarking. Kluwer’s International Series, p.13.