Kayvan Moradia, Marko M. Melandera,∗
aDepartment of Chemistry, Nanoscience Center, University of Jyv¨askyl¨a, P.O. Box 35, Jyv¨askyl¨a,FI-40014, Finland
Abstract
Semiconductor electrodes (SCEs) play a decisive role in e.g.clean energy conversion technologies but understanding their complex electrochemistry remains an outstanding challenge. Herein, we review electronic structure methods for describing the applied electrode potential in simulations of semiconductorelectrolyte interfaces. We emphasize that inclusion of the electrode potential
is significantly more challenging for SCEs than for metallic electrodes because SCEs require accurate models of semiconductor capacitance, including the space-charge region and surface effects, as well as the electrolyte double-layer capacitance. We discuss how these physicochemical complications challenge the development of atomistic models of SCE and how they impact the applicability of the computational hydrogen electrode, capacitance correction, grand canonical DFT, and Green function methods to model SCEs. We highlight the need for continued methodological development and conclude that integrating advanced atomistic models of SCEs with grand canonical, constant inner potential DFT or Green function methods holds promise for accurate SCE simulations.
Keywords: Semiconductor electrodes, Grand canonical DFT, Computational hydrogen electrode, Capacitance corrections, Green’s function, Constant potential, Electrode potential
∗Corresponding author
Emailaddress:marko.m.melander@jyu.fi (Marko M. Melander)
PreprintsubmittedtoCurrentOpinioninElectrochemistry October8,2024
1. Introduction
Semiconductor electrodes (SCEs) play a crucial role in (photo)electrochemistry, particularly in devices used for photoelectrochemical energy conversion andstorage applications.[1, 2] Despite many alluring applications, atomic-scaleunderstanding on the factors defining the (photo)electrochemical performance of SCEs remains far from that of metallic electrodes as SCEs exhibit more nu anced electronic structure features due to the presence of a band gap, possible polaronic and surface states, and doping effects, for instance.[3, 4, 5, 6] Also, the electrode-electrolyte interfaces are more complex than those on metallic electrodes due to the pronounced role of surface states and acid-base chemistry on oxide surfaces, for example. Furthermore, the low number of charge carriers leads to features such as the spatially extended space-charge region (SCR) and band bending. Finally, in the case of electrochemistry, all these effects depend on the applied electrode potential.[6, 7, 8] Overall, simulating these electronic and structural effects requires the use of more refined electronic structure methods and atomistic models than needed for metals. Currently, our understanding on how the atomic-scale properties of SCEs depend on the applied electrode potential, electrolyte, and electrode structure is far from complete and new theoretical and computational methods are needed to provide such understanding. In this article, we will focus on the first challenge; how to model the impact of an applied electrode potential in semiconductor electrochemistry using electronic structure methods. We have made a deliberate choice not to discuss the simulation of the electrolyte or out-of-equilibrium effects, such as light illumination or current. Within these restrictions, we are primarily interested in the merits and limitations of currently available computational approaches to model the applied electrode potential within density functional theory (DFT). Besides ground state DFT, we will briefly discuss the use of Green’s function approach for describing the electrode potential.
2. The applied potential in semiconductor electrodes: Implications for electronic structure methods
Electrode potential is the central quantity in all electrochemical systems. Experimentally, the electrode potential applied to the working electrode is measured against a well-defined reference electrode but in atomistic DFT simulations it is more convenient to work on a single or ”absolute” electrode potential scale.[9] On the single electrode potential scale the applied electrode potential is directly proportional to the electrochemical potential of electrons withinthe electrode. The general equation for the single electrode potential is[10, 11]
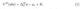
where the standard chemical potential of electrons ( µe) is an intrinsic material property and independent of the electrode potential ϕ stands for the inner potential difference, i.e.the electrostatic potential difference between the bulk of electrode (M) and solution (S) as depicted in Figure 1. Kis a constant defining the reference scale, which in DFT simulations has been realized in two ways. The most conventional choice in DFT calculations is to reference the single electrode potential against the electrostatic potential in vacuum or the bulk part of an explicit or implicit solvent. With this choice, the single electrode potential is [10, 12]
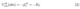
where EFis the Fermi level of the DFT system. An equally valid option for Kis to reference it against ”free” electron in solution.[10, 11] When setting the electrostatic potential bulk solution to zero through the use of Dirichlet boundary conditions, the single electrode potential is given by[4]
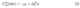
which allows direct control over the electrode potential through ∆Sϕ without explicitly introducing the Fermi level.[4] Equations (1)-(3) together show that the electrode potential is directly related to the electrochemical potential of electrons within the electrode bulk
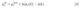
where µe is an intrinsic bulk material property while the activity of electrons (ae(r)) and the inner potential (ϕ(r)) vary spatially. For metallic electrodes, the activity term is usually omitted but it plays a crucial role in SCEs due to the low number of charge carriers which in turn leads to poor screening of the interfacial charge and the creation of a SCR. In particular, ae(r) and ϕ(r) are correlated because under equilibrium conditions µ˜e is constant throughout the system: this coupling leads to local variations in the electrostatic potential and charge distribution within the SCR[7] as shown in Figure 1. It should also be stressed that the applied electrode potential is a bulk property and it is therefore measured from the ”backside” or bulk of the SCE. This means that the electrode potential needs to be measured outside the SCR, i.e.when the bulk values of ϕMand aehave been reached, see Figure 1.
3. A DFT perspective on modelling semiconductor electrodes
As the physical and chemical properties of SCEs differ significantly from those of metallic electrodes, also the modelling approaches are distinctly different. The most immediate differences between metallic and semiconducting electrodes are related to their qualitatively different electronic structures. Metals have a continuous electronic structure without any energy separation between the filled and empty electronic states (bands) while in semiconductors an energy gap separates the occupied (valence) bands from the empty (conduction) bands as shown in Figure 1. The presence of a band gap in SCEs means that the Fermi-level, and hence the absolute potential on the vacuum scale (Eq.(2)), cannot be varied continuously in standard DFT approaches using surface slab models while this is possible experimentally and through the advanced DFT models. Furthermore, it is well known that capturing the band gap, even qualitatively, with DFT requires the use of more advanced functionals than those needed for metallic systems. Typically, functionals that improve the description of localized electrons or strong electronic correlation, such as +U-corrected, meta-GGA, or hybrid functionals, are needed.[14] Be- sides the functional choice, the number of k-points used for sampling the electronic structure in the reciprocal space needs to be handled with care, because SCEs seem to require substantially higher k-point densities than metals to accurately model the band gap region.[15] However, capturing the band gap is not enough as the edges of the valence and conduction band electronic levels need to be correctly aligned with respect to a reference state, often the vacuum as shown in Figure 1. This is of crucial importance as the absolute energy level positions directly impact the SCE’s electrode potential on the absolute electrode potential scale[12] as can be seen from Eq. (2). Most SCEs of practical interest are not intrinsic semiconductors but they are often doped with foreign atoms to improve their conductivity or other physical and chemical properties. The introduction of dopants has a direct

Figure 1: Depiction of important concepts and phenomena of SCEs. Top) A simplified energy diagram of a semiconductor–solvent–vacuum system. The darker grey area within the semiconductor shows the space-charge region (SCR). The dashed lines and ϕ(r) denotes the spatially varying electrostatic potential. ϕV, ϕS, and ϕM are the vacuum, solvent, and electrode inner potentials, respectively. EF is the Fermi level. EC and EV are the conduction and valence band energies, respectively. Their spatial variations correspond to band bending. ∆Egap is the band gap. Center) Mechanisms of polaron and surface state formation, and their on the electronic structure as a function of potential. The DOSs are computed for an anatase TiO2(101) surface using CIP-DFT.[13] Bottom) Fermi-pinning and state of occupancy as a function of the applied potential. The empty (filled) surface states are marked with white (black) dots. The effects of pinning on the surface charge (σSS) and capacitance (CSS) as a function of potential are also schematically shown.
impact on the SCEs’ electronic structure as new electronic states are created. The SCE electronic structure can be also be modified by the presence of polaronic states, i.e.localized electronic states where either an electron or hole becomes spontaneously trapped on a single or few atoms due to lattice distortions. Finally, near an SCE surface, specific surface states may appear due to breaking of the 3D periodicity. When the concentration of surface states is high and when their energy levels fall in the band gap, the Fermi level may remain efficiently fixed at these energies. As a result, the surface becomes charged and most of the electrostatic potential drop takes place on the electrolyte side while the drop within this SCR remains rather unchanged as the electrode potential is applied. This phenomenon is known as Fermi-pinning, which means that the Fermi level, the inner potential, and the electrode potential remain essentially fixed while the surface charge can be drastically changed.[16] Because the Fermi level at equilibrium is aligned with the redox potential of the electrolyte species, Fermi-pinning has a crucial impact on the reactivity of SCEs.
From a DFT perspective, an accurate treatment of dopant, polaron, sur- face, and other defect states as function of the electrode potential is required to understand how defects modify the SCEs’ properties. For instance, the potential-dependent formation of polaronic states has been shown to greatly impact the electrochemical thermodynamics and kinetics of SCEs[13] while the localized surface states fundamentally change the proton-coupled electron transfer chemistry at metal-oxide surfaces.[17, 18] Furthermore, polaronic and surfaces states change the differential capacitance and e.g.Fermipinning leads to a sharply peaked differential capacitance (CSS, Eq. (10)) around the electrode potential where the surface states become occupied as shown in Figure 1.[16]
Metallic and semiconducting electrodes also differ in their electronic screening properties. Metals typically carry charge and screen interfacial fields or charge very efficiently due to the high concentration of delocalized electrons. In SCEs, however, the electrons are more tightly bound and localized in the valence band. Therefore, the concentration of free charge carriers in semiconductors is low and this leads to low conductivity and poor screening of interfacial charges and electrostatic potential differences. Due to their widely different screening properties, metallic and semiconducting electrodes behave very differently when brought into contact with an electrolyte and when an electrostatic potential difference across the interface is created. On metallic electrodes, the potential drop takes place almost entirely on the electrolyte side because the electrostatic potential is efficiently screened by the metal. However, in SCEs, the electrostatic potential is inefficiently screened by the electrode surface and the potential drop within the SCE is extended through out a SCR. The SCR is analogous to the electrochemical double layer formed on the electrolyte side of the electrochemical interface and features an imbalance of charges until the surface charge is fully screened in the SCE bulk region. The width of the SCR depends on the dopant concentration but for a typical doping concentration of 1017 dopants/cm3 the SCR spans 100µm.[19] The imbalance of charges is coupled with the spatially varying electrostatic potential and field within the SCR (see Eq. (4)). Therefore, the band energies within the SCR also differ from the bulk semiconductor; this is known as band bending, which significantly impacts the electrochemical properties of SCEs. Additionally, interactions between the SCE and the electrolyte may shift the band edges, and capturing this necessitates careful modelling of the SCE–electrolyte interface.
The bulk region of a SCE is only reached after the surface charge has been completely screened by the SCR and this SCR significantly complicates the DFT modelling SCEs. In particular, because the space charge thickness for a typical doping concentration of 1017 dopants/cm3 is 100µm,[19] extremely large slab models and simulation cells are needed to capture the SCR. This is particularly so for simulating the electrode potential of SCEs because the applied electrode potential is defined within the electrode bulk and measured from the backside of the electrode as was stressed in the previous section; this means that the entire SCR needs to be surpassed before the electrode potential can be defined.
The DFT treatment of SCEs with a low charge carrier concentration is particularly difficult as the extent of the SCR prevents a fully DFT description of an entire SCE. To overcome this difficulty, DFT-based multiscale models have been developed. The quantum-continuum approaches[3, 20, 21, 22] combine a surface DFT model with a continuum dielectric description of the SCR and SCE bulk. The spatial charge carrier and electrostatic potential distributions are described through different Poisson-Boltzmann models which treat the charge within the SCR either as a planar charge plane[20], homogeneous background,[21] or Poisson-Boltzmann -like counter charge distribution.[3, 22] Alternatively, the SCR can be modelled through an electrostatic embedding approach where a DFT cluster model of the surface is hierarchically embedded in various electrostatic descriptions of the bulk SCE. Both the quantum-continuum and embedding approaches can be naturally combined with either an implicit or explicit electrolyte model and can describe the electrostatic potential both within the SCR and in the bulk; this allows the description of the electrode potential by using the solvent reference (Eq. (3)) as has been explicitly demonstrated in continuously quantum-continuum approaches.[3, 22] However, both the quantum-continuum and embedding approach require substantial implementation work and custom modifications to the underlying DFT code.
Highly-doped SCEs are significantly simpler to simulate as they are modelled through DFT alone by using “pseudoatoms” which carry fractional nuclear charges in specially constructed pseudopotentials. [23]. This construction allows for the study of surface and polaronic states, doping, band bending, the SCR, and approach to bulk of highly doped SCEs using DFT alone and with minimum implementation efforts or increases in computaional cost. Notably for electrochemistry and controlling the electrode potential, the pseudo-atom approach allows shifting the bulkFermi level continuously even within the band gap and can be combined with either an implicit or explicit electrolyte model.
4. Computational hydrogen electrode model
Computational Hydrogen Electrode (CHE) is a widely-used theoretical framework used for modelling the electrochemical thermodynamics of protoncoupled electron transfer reactions. CHE describes the impact of the electrode potential and pH implicitly by referencing the proton and electron electrochemical potentials against the standard hydrogen electrode using the SHE. Hence, at 0V vs SHE, the free energy of the proton-electron couple can replaced by the free energy of hydrogen gas under standard conditions. Under other pH and potential values, the free energies are simply shifted by the proton activity and electrode potential terms, which allows writing the free energy changes of any electrochemical proton-coupled electron transfer step on the SHE scale as:
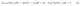
which shows that CHE accounts for the influence of the pH and potential conditions aposteriorias linear corrections on the free energy computed under standard conditions.
CHE has been widely applied to simulate electrochemical thermodynamics on metallic and SCEs.[24, 25, 26] Notably, the CHE formalism remains unchanged when adopted to simulate SCEs.[27] However, CHE has several limitations that arise from its underlying assumptions. CHE assumes fully
concerted proton-coupled electron transfer, meaning that protons and electrons transfer simultaneously, and therefore pure electron transfer, proton transfer, and chemical steps as a function of potential cannot be addressed. [28] Furthermore, only reaction thermodynamics can be treated and kinetics need to be computed using other approaches.[29] Because the electron and proton chemical potentials do not explicitly affect the DFT calculation, CHE cannot account for potentialand pH-dependent changes in the surface charge, electronic structure, and the mechanism, for instance. In particular, CHE assumes that the surface remains uncharged and thereby cannot account for surface charging effects[30] or non-Nernstian effects arising from surface charge and dipole-field interactions.[25] In the case of SCEs, neglecting the explicit surface charging effects means that CHE cannot be applied to study the impact of the SCR or polaronic and surface states as a function of the potential.
5. Canonical DFT and capacitance models
DFT simulations of electrochemical systems can be performed either within the canonical, constant charge or grand canonical, constant potential ensembles. In canonical DFT, one performs constant charge calculations for a range of charges or number of electrons (Ne) to obtain the canonical free energy as a functional of the thermal density operator and as a function of electrons: F[ρˆ; Ne] = F(Ne). The conversion to constant potential energy, i.e. grand free energy, is achieved through a Legendre transform:
Ω[ρˆ; µ˜e] = F(Ne) − µ˜eNe. If F(Ne) and Ω(µ˜e)
are convex, the Legendre transform is unique and bijective, and therefore electrochemical DFT calculations performed in either the canonical or grand canonical ensemble yield the same thermodynamic expectation values and are equally valid in theory– this is the important concept of ensemble equivalence.[31]
The ensemble equivalence has been recently reaffirmed by numerical simulations, which show that the grand canonical and canonical ensembles converge in the infinite surface size limit.[32, 33, 34] These works have also shown that the canonical free energy as a function of charge or the potential can be written in terms of the potential-dependent differential capacitance C(µ˜e)
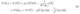
where N0 is the charge at a reference electrode potential, often chosen as the potential of zero charge, and µ˜eis the change in the electrode potential with respect to this reference.[34] Notably, the capacitance models provide an easy-to-apply and widely-applied electrochemical DFT approach but a good model for the capacitance as a function of potential is needed for accurate results.[32, 33] Because in the case of metallic electrodes the differential capacitance is mainly due to the electrolyte, a good model of the electrolyte capacitance has been deemed sufficient to successfully apply Eq. (6) to metallic electrodes.[32, 33]
However, when it comes to modeling SCEs, a good model for the electrolyte capacitance is not enough as the electrode itself significantly influences the capacitance.[34] In particular, the total capacitance at the semiconductor-electrolyte interface (CSCE) depends on both the semiconductor surface (CSC) and the electrochemical double layer contributions (CDL):

The CSCneeds to account for both the SCR and surface effects. Therefore, the equivalence of grand canonical and canonical ensemble methods cannot be established by interpolating to the infinite surface size limit in the surface xy-plane only but one also needs to interpolate to the infinite slab thickness limit in the z-direction to capture the capacitive contributions in this direction.[34, 35] Indeed, our recent work shows that four-layer metallic slabs are sufficient for modeling metallic electrodes whereas a SCE requires a much thicker slab to exhibit convergence.[4] In general, one needs to account for the influence of both the surface/polaronic states (CSS) as well as the SCR (CSCR) contributions on the semiconductor capacitance (CSC)
CSC= CSCR+ CSS (8)
where CSCRfollows the Mott-Schottky (MS) relation of an ideal SCE with only SCR capacitance,[8]
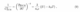
plicated as the charge within the SCR (qSCR) depends on the dopant concentration (nb), dielectric constant (ϵ), temperature T, and the electrode potential Uin units of eV.[35] The MS model is based on a simple band-bending scenario without considering surface or polaronic states[36], which leads to deviations from this ideal behavior. Surface states can significantly impact the capacitance at SCE interfaces,[18] particularly in systems with high surface state concentrations, and thereby introduce additional capacitive contributions (CSS):
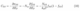
where σSS is the surface charge, NSS is the number density of surface
states per area, and fSS(ESS) = h is the Fermi-Dirac distribution for the surface states at energies ESS. CSSdepends sensitively on the energy distribution of the surface states and their occupancy; the quantum capacitance[37] directly links density of surface states (DSS) to the surface state capacitance: DSS(EF) = CSS. As DSScan be influenced by multiple factors such as doping, applied potential, and surface adsorption processes, CSSis expected to be extremely complex; this has been exemplified for CuGaS2 electrodes, where the CSSdominates in certain potential ranges and leads to significant, non-linear, and non-trivial deviations from the ideal
MS behavior.[35]
The importance of the different capacitive contributions to Eq. (7) and (8) depends on both the electrode material, electrolyte, and the electrode potential. For SCEs, CDL ≫ CSC is often observed and the contribution of the double-layer capacitance is often neglected.[38] For metallic electrodes the opposite is true and CDL ≪ Cmetal, and it is enough to consider just the double-layer capacitance.[34] However, general models of the semiconductor- electrolyte interface capacitance require accounting for all the contribution of CSCR, CSS, and CDL. From the DFT perspective, this means that convergence and extrapolation to the thermodynamic limit need to be achieved for both the surface size and the SCE thickness. As of yet, we are not aware of any DFT studies or atomistic models that would have successfully reproduced the complex SCE capacitance. Resolving this issue requires adopting and refining the atomistic models of the SCEs as well as experimental capacitance measurements on well-defined electrodes to understand the SCE capacitance and to establish the accuracy of the capacitance models.
6. Grand canonical DFT
Grand canonical DFT (GC-DFT)[39] describes the grand free energy of an electrochemical system as an explicit functional of the grand canonical density operator, which depends on the electrochemical potential of electrons. GC-DFT thereby offers an exact treatment of electrochemical thermodynamics as function of the electrode potential: Ω[ρˆ˜µe; µ˜e] = Ω(µ˜e).[40] Currently, GC-DFT implementations are available in various solid state DFT packages and can be rather routinely used for studying metallic systems as a function of potential.[41] Most GC-DFT implementations[41] use either the Fermi- level or the work function to model the single electrode potential on the vacuum scale (Eq. 2). Using the Fermi level to account for the electrode potential is, however, problematic with currently used slab models because the Fermi level cannot be continuously altered across the band gap region.[4, 42] The use of the recent constant inner potential (CIP-)DFT[4] circumvents this difficulty and allows continuous control over the electrode potential on the solvent reference scale (Eq. (3)).
Thus far, the GC-DFT has been mostly used for studying metallic electrodes while studies on SCEs remain limited. Yet, it has been shown that at least the CIP-DFT can model e.g.polaron formation, Fermi-pinning, and reaction thermodynamics and kinetics as a function of potential.[13] However, all GC-DFT studies have used standard DFT slab models of the SCE and the more advanced atomistic models in such quantum continuum approximations have not been used but it is already known that SCEs require significantly thicker slab models than metallic systems. Initial tests have shown that an 8-layer SCE model does not provide a converged inner potential with respect to slab thickness.[4] However, absolute convergence might not be required for GC-DFT to be useful and we have shown that a good agreement with experiments on the electrode potential at which surface polarons appear on TiO2 can be reached by using a 4-layer slab model with CIP-DFT.[13] Yet, the slow convergence with respect to slab thickness is to not only a numerical but also a theoretical issue as discussed in Ref. [4]. In particular, the grand canonical and canonical ensembles may yield different expectation values for SCEs – this would mark a rare occurrence of ensemble non-equivalence, i.e. a situation where canonical and grand canonical calculations yield different results in contrast to the expected equivalence discussed in the previous section.
In general, we do not yet know how thick slabs are needed to provide a fully converged description of the SCE and the SCR. We nevertheless expect that GC-DFT calculations with an accurate description of the SCR within standard slab models of SCEs will be prohibitively expensive. We therefore suggest combining GC-DFT with the advanced DFT models to model SCE as an explicit function of the potential. As e.g.quantum continuum models can be used to compute the electrostatic potential across the SCR and in the bulk in, we consider that the use of CIP-DFT with these models will enable accurate GC-DFT simulations of the applied potential in SCEs.
7. Green function methods
While most electronic structure studies on semiconductor surfaces have relied on the use of slab models and DFT, SCEs can also be modelled as semi-infinite surfaces using DFT-based Green function approaches.[43] The Green function methods treat the semiconductor surface as part of a semi- infinite device consisting of bulk, surface, and vacuum regions. The bottom- side of the surface is connected to the semiconductor bulk through electrostatic boundary conditions and a self-energy matrix while the top-side surface is connected to vacuum-like pseudoelectrode modelled through electrostatic boundary conditions. The configuration leads to solving a matrix equation of the entire device and yields a self-consistent solution for the electronic density and energy.
A particular advantage of the Green function approach is that thinner surface models are needed to obtain fully converged surface energies and work functions. For electrochemical system, the Green function approach is the only currently available method which allows direct control over the bulk Fermi level; because the semiconductor bulk Fermi level is an input to the model, as in the case of GC-DFT, the Green function method guarantees that the relevant bulk Fermi level is used as the absolute electrode potential (Eq.(2)). It has also been shown that the method can model e.g. band bending, the SCR, and surface states at different dopant concentrations and as a function of the Fermi level. Despite these attractive features, the method has not, however, been applied to study SCEs. We believe that this is because the method requires the use of a localized (LCAO) basis set and has only been implemented in the proprietary QuantumATK software used mainly in the semiconductor industry. Currently, dielectric electrolyte models have not been included in QuantumATK, which limits the use of the Green function method for SCEs. Finally, implementing both localized orbitals and the Green function method in widely used plane wave DFT codes would require significant development work.
8.Conclusions
We have reviewed electronic structure methods for describing the influence of the electrode potential in semiconductor electrochemistry. First, we discussed the formal definition of electrode potential as the bulkFermi level or inner potential. Then, we addressed in detail which physicochemical features complicate the DFT modelling of semiconductor electrodes – these are collected in Figure 1. We emphasized the difficulty and importance of including various defect states and the space-charge region in electronic structure calculations. In particular, without accurate models of the SCR, one cannot model the semiconductor bulk and thereby define the electrode potential. After addressing various atomistic models of SCEs, we discussed different electronic structure methods for simulating SCEs as a function of the electrode potential. It was emphasised that while the computational hydrogen electrode method is simple to use, it cannot describe for instance the impact of potential-dependent defect, surface, or polaron states or the SCR. While electrostatic or capacitance corrections on canonical DFT are in principle ex- act ways of including the electrode potential effects, their usefulness is limited by the lack of accurate semiconductor capacitance models or experimental data. In particular, the capacitance corrections should account for the presence of defect/surface/polaronic states and the SCR (see Figure 1) and it is not enough to have a good model of the electrolyte capacitance because the semiconductor capacitance often dominates the total capacitance. Data on well-defined test systems is needed to make capacitance corrections useful, and capacitance data on single-crystal SCEs at different dopant concentrations would be particularly valuable. We also pointed out that in addition to interpolating to infinite surface sizes in metallic systems, SCEs require interpolation to infinite simulation cell thicknesses as well, and this interpolation is expected to converge slowly due to the extended SCR.. In discussing GC-DFT simulations of SCEs as an explicit function of the electrode potential, we highlighted that very thick slab models are to achieve fully converged calculations and highlighted the utility of the recent CIP-DFT approach. We also reviewed the use of DFT with Green function theory for simulating SCE in a semi-infinite surface setup and emphasized that this is the only model that enables genuine control over the electrode (bulk) Fermi level. While multiple electronic structure methods and atomistic models have been developed and applied to simulate semiconductor electrochemistry, this area remains highly challenging and no method can yet be considered generally accepted or applicable. This calls for further methodological develop-ment and implementation; we consider that the Green function methods with a fully explicit description of SCEs or the combination quantum-continuum models combined with CIP-DFT appear particularly promising.
9.Acknowledgements
The authors acknowledge the financial support by the Academy of Finland (grant number #338228).
References
[1] K. Moradi, M. Ashrafi, A. Salimi, M. Melander, Hierarchical MoS2@
NiFeCo-Mo (doped)-LDH heterostructures as efficient alkaline water
splitting (photo) electrocatalysts, ChemRxiv (2024).
[2] J. Lv, J. Xie, A. G. A. Mohamed, X. Zhang, Y. Wang, Photoelectro-
chemical energy storage materials: design principles and functional de-
vices towards direct solar to electrochemical energy storage, Chemical
Society Reviews 51 (4) (2022) 1511–1528.
[3] Q. Campbell, I. Dabo, Quantum-continuum calculation of the surface
[4] M. M. Melander, T. Wu, T. Weckman, K. Honkala, Constant inner
potential dft for modelling electrochemical systems under constant po-
tential and bias, npj Computational Materials 10 (1) (2024) 5, **This
work develops a grand canonical DFT model which allows direct control
over the bulk inner potential.
15
[5] S. A. Akhade, N. J. Bernstein, M. R. Esopi, M. J. Regula, M. J. Janik, A
simple method to approximate electrode potential-dependent activation
energies using density functional theory, Catalysis Today 288 (2017) 63
[6] M. R. Nellist, F. A. Laskowski, F. Lin, T. J. Mills, S. W. Boettcher,
Semiconductor–electrocatalyst interfaces: theory, experiment, and ap-
plications in photoelectrochemical water splitting, Accounts of chemical
research 49 (4) (2016) 733–740.
semiconductor/electrolyte junctions, J. Phys. Chem. Lett. 5 (1) (2014)
205–207. doi:10.1021/jz402703d.
[8] R. Memming, Semiconductor Electrochemistry, WILEY-VCH Verlag
[9] L. Andersson, C. Zhang, Molecular dynamics simulations of metal-
electrolyte interfaces under potential control, Current Opinion in Elec-
trochemistry 42 (2023) 101407, ** Gives a detailed account on methods
for controlling the electrode potential in atomistic simulations.
[10] S. Trasatti, The absolute electrode potential: The end of the story,
Electrochim. Acta 35 (1) (1990) 269 – 271.
[11] S. Trasatti, The absolute electrode potential: an explanatory note (rec-
ommendations 1986), J. Electroanal. Chem. Interfacial Electrochem.
209 (2) (1986) 417 – 428.
[12] J. Cheng, M. Sprik, Alignment of electronic energy levels at electro-
chemical interfaces, Phys. Chem. Chem. Phys. 14 (2012) 11245–11267.
[13] T. Wu, M. M. Melander, X. Guo, G. Zhang, Y. Zhang, Z. Wang, L. Song,
Z. Liu, J. Xiong, K. Honkala, Potential-dependent polaron formation
activates tio2 for the hydrogen evolution reaction, ChemRxiv** A CIP-
DFT description of a semiconductor electrode and demonstration of
potential-dependent polaron formation. (2024). doi:10.26434/chemrxiv-
2024-j7thd.
[14] A. Ghosh, S. Jana, T. Rauch, F. Tran, M. A. L. Marques, S. Botti,
H. Oschinski, N. G. H¨ormann, K. Reuter, Constant potential energetics of metallic and semiconducting electrodes: A benchmark study on 2D materials, The Journal of Chemical Physics 160 (21) (2024) 214706, * Detailed work on GC-DFT applied to 2D semiconductor electrodes.
A. J. Bard, A. B. Bocarsly, F. R. F. Fan, E. G. Walton, M. S. Wrighton, The concept of fermi level pinning at semiconductor/liquid junctions. consequences for energy conversion efficiency and selection of useful solution redox couples in solar devices, Journal of the American Chemical Society 102 (11) (1980) 3671–3677.
R. E. Warburton, A. V. Soudackov, S. Hammes-Schiffer, Interfacial proton-coupled electron transfer via localized trap states on metal oxide surfaces, The Journal of Physical Chemistry C 128 (19) (2024) 7903–
7912.
B. Klahr, S. Gimenez, F. Fabregat-Santiago, T. Hamann, J. Bisquert, Water oxidation at hematite photoelectrodes: The role of surface states, Journal of the American Chemical Society 134 (9) (2012) 4294–4302.
R. Memming, Semiconductor Electrochemistry, WILEY-VCH, Weinheim, 2000.
O. Sinai, O. T. Hofmann, P. Rinke, M. Scheffler, G. Heimel,
L. Kronik, Multiscale approach to the electronic structure of doped semiconductor surfaces, Phys. Rev. B 91 (2015) 075311. doi:10.1103/PhysRevB.91.075311.
URL https://link.aps.org/doi/10.1103/PhysRevB.91.075311
S. Erker, P. Rinke, N. Moll, O. T. Hofmann, Doping dependence of the surface phase stability of polar O-terminated (000¯1) ZnO, New Journal of Physics 19 (8) (2017) 083012.
Q. Campbell, Voltage-dependent first-principles simulation of insertion of chloride ions into Al/Al2O3 interfaces using the quantum continuum approximation, Journal of The Electrochemical Society 170 (3) (2023)
031506, **Application of the quantum continuum approximation to an
electrochemical reaction.
[23] O. Sinai, L. Kronik, Simulated doping of si from first prin-
ciples using pseudoatoms, Phys. Rev. B 87 (2013) 235305, **
An efficient DFT model highly doped semiconductor electrodes.
doi:10.1103/PhysRevB.87.235305.
URL https://link.aps.org/doi/10.1103/PhysRevB.87.235305
[24] A. Groß, Reversible vs standard hydrogen electrode scale in interfacial
electrochemistry from a theoretician’s atomistic point of view, The Jour-
nal of Physical Chemistry C 126 (28) (2022) 11439–11446.
[25] A. M. Verma, L. Laverdure, M. M. Melander, K. Honkala, Mechanistic
origins of the ph dependency in au-catalyzed glycerol electro-oxidation:
Insight from first-principles calculations, ACS Catalysis 12 (1) (2022)
] S. D. Beinlich, G. Kastlunger, K. Reuter, N. G. Ho¨rmann, Controlled
electrochemical barrier calculations without potential control, Journal
of Chemical Theory and Computation 19 (22) (2023) 8323–8331.
A´. Vald´es, J. Brillet, M. Gra¨tzel, H. Gudmundsdo´ttir, H. A. Hansen,
H. J´onsson, P. Klu¨pfel, G.-J. Kroes, F. Le Formal, I. C. Man, R. S. Martins, J. K. Nørskov, J. Rossmeisl, K. Sivula, A. Vojvodic, M. Z¨ach, Solar hydrogen production with semiconductor metal oxides: new directions in experiment and theory, Phys. Chem. Chem. Phys. 14 (2012) 49–70.
[28] A. M. Verma, K. Honkala, M. M. Melander, Computational screening
of doped graphene electrodes for alkaline CO2 reduction, Frontiers in
Energy Research 8 (2021).
[29] M. M. Melander, Grand canonical ensemble approach to electrochemical
thermodynamics, kinetics, and model hamiltonians, Curr. Opin. Elec-
trochem. 29 (2021) 100749.
[30] S. Ringe, The importance of a charge transfer descriptor for screening
potential CO2 reduction electrocatalysts, Nature Communications 14 (1)
(2023) 2598.
18
[31] H. Touchette, The large deviation approach to statistical mechanics,
Physics Reports 478 (1) (2009) 1–69.
[32] N. G. Ho¨rmann, S. D. Beinlich, K. Reuter, Converging divergent paths:
Constant charge vs constant potential energetics in computational elec-
trochemistry, The Journal of Physical Chemistry C 128 (13) (2024)
5524–5531.
33] G. Kastlunger, S. Vijay, X. Chen, S. Sharma, A. Peterson, On the ther-
modynamic equivalence of grand canonical, infinite-size, and capacitor-
based models in first-principle electrochemistry, ChemPhysChem 25 (10)
(2024) e202300950.
[34] F. Dom´ınguez-Flores, M. M. Melander, Approximating constant poten-
tial DFT with canonical DFT and electrostatic corrections, The Journal
of Chemical Physics 158 (14) (04 2023).
[35] B. Miao, K. Sangar´e, A. Iqbal, B. Marsan, K. H. Bevan, Interpreting
interfacial semiconductor–liquid capacitive characteristics impacted by
surface states: a theoretical and experimental study of CuGaS2, Phys.
Chem. Chem. Phys. 22 (2020) 19631–19642, * Important work on the
interpretation of semiconductor electrode capacitance.
[36] M. H. Dean, U. Stimming, Capacity of semiconductor electrodes with
multiple bulk electronic states part i. model and calculations for discrete
states, Journal of Electroanalytical Chemistry and Interfacial Electro-
chemistry 228 (1) (1987) 135–151.
[37] T. Binninger, First-principles theory of electrochemical capacitance,
Electrochimica Acta 444 (2023) 142016.
[38] W. Schmickler, E. Santos, Interfacial electrochemistry, 2nd edition,
562 Springer, 2010.
[39] N. D. Mermin, Thermal properties of the inhomogeneous electron gas,
Phys. Rev. 137 (1965) A1441–A1443.
[40] M. M. Melander, M. J. Kuisma, T. E. K. Christensen, K. Honkala,
Grand-canonical approach to density functional theory of electrocat-
alytic systems: Thermodynamics of solid-liquid interfaces at constant
ion and electrode potentials, J. Chem. Phys. 150 (4) (2019) 041706.
19
[41] S. Ringe, N. G. H¨ormann, H. Oberhofer, K. Reuter, Implicit solva-
tion methods for catalysis at electrified interfaces, Chem. Rev. 122 (12)
(2022) 10777–10820.
[42] C. Islas-Vargas, A. Guevara-Garc´ıa, M. Galva´n, Electronic structure be-
havior of PbO2, IrO2, and SnO2 metal oxide surfaces (110) with dissocia-
tively adsorbed water molecules as a function of the chemical potential,
J. Chem. Phys. 154 (7) (2021) 074704.
[43] S. Smidstrup, D. Stradi, J. Wellendorff, P. A. Khomyakov, U. G. Vej-
Hansen, M.-E. Lee, T. Ghosh, E. Jo´nsson, H. Jo´nsson, K. Stokbro, First-
principles green’s-function method for surface calculations: A pseudopo-
tential localized basis set approach, Phys. Rev. B 96 (2017) 195309, **
This work develops a DFT-based Green function approach for simu-
lating a semi-infinite surface with a direct control over the bulk Fermi
level.





